本篇旨在记录自己学习L*算法的过程和理解。 参考：

1. 吴礼发老师的《网络协议逆向分析及应用》
2. L*算法创世文：Learning Regular Sets from Queries and Counterexamples*
3. 基于米利机的LM*算法：Reverse Engineering Enhanced State Models of Black Box Software Components to support Integration Testing
4. 关于Model Learning的综述：Model Learning: A Survey on Foundation, Tools and Applications
5. 对L*算法的理解和优化：Insights to Angluin’s Learning
6. 找到的唯一一篇中文对L*算法的解释：模型学习 Angluins L*算法 学习笔记-wcventure

基础

1. 集合

集合连接：A·B

集合A={0,01}, B={1,10} A·B = {01,010,011,0110}

克林闭包

Σ是一个字母表集合，克林闭包（kleene Closure）Σ*=Σº∪Σ¹∪Σ²∪…，即Σ上所有字符串的集合。 如：{0,1}* = {ε，0，1，00，01，11，000，001，010，011，100，…}

2. 名词解释（自动机相关）

• alphabet 字母表：符号的有限集合。 记作： Σ 例如：{a, b, … , x, m}
• strings 字符串： 通常我们用到建立在 Σ 上的字符串：有穷的符号序列。 例如：对于 Σ={a, b, c}, “ababc” 就是 Σ 上的一个字符串。
• languages 语言：通常我们也只用建立在Σ上的语言，语言就是多个字符串的集合。例如 {ababc, ab, bc, ..}
• sentences 句子：句子是语言集合中元素（字符串）的另一个称呼。
• notation 符号：Σ* 是Σ上所有可能的字符串的集合。例如：Σ={a, b}, Σ* = { ε, a, b, ab, ba}

正则语言

我的理解：一个正则语言L是一个字母表克林闭包集合的一个子集。一个正则语言可以用一个确定有限自动机（DFA）来表示。

前缀/后缀闭合

• 前缀闭合：对于一个string集A，如果A是前缀闭合的，当且仅当A中每个成员的每个前缀也是这个集合的成员之一。
• 后缀闭合：对于一个string集A，如果A是后缀闭合的，当且仅当A中每个成员的每个后缀也是这个集合的成员之一。

3. 确定有限状态自动机（DFSM、DFA）

确定有限自动机A是由：

• 一个非空有限的状态集合Q
• 一个输入字母表Σ（非空有限的字符集合）
• 一个转移函数δ: Q×Σ->Q，例如：δ(q,σ)=p (p,q∈Q, σ∈Σ)
• 一个开始状态q0∈Q
• 一个接受状态的集合F∈Q

所组成的5元组。表示为A = (Q,Σ,δ,q0,F)。一个正则语言可以用一个DFA表示。如：

• 正则语言表示：L为长度为偶数的字符串组成的正则语言
• DFA表示：状态机只接受长度为偶数的字符串，拒绝其它所有长度类型的字符串

DFA状态转换图如下：

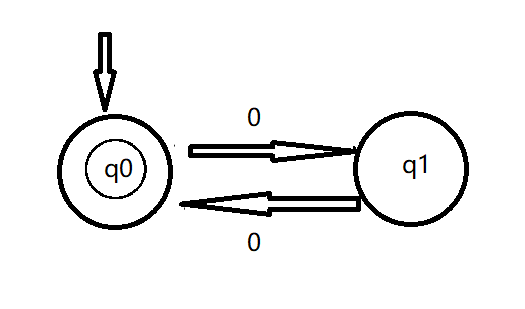
q0为初始状态，也为状态机最终接受的终止状态。

4. 米利型有限状态机（Mealy Machine）

在DFA的基础上添加了输出（output），由六元组组成：(Q,I,O,δ,λ,q0)，构成自：

• 非空有限状态集Q
• q0∈Q为初始状态
• I为有限输入符号集
• O为有限输出符号集
• δ: Q×I->Q 为状态转移函数
• λ: Q×I->O 为输出函数

相比于DFA，Mealy Machine将DFA中的Σ划分为有限输入输出符号集I/O，并增加了输出函数λ，状态迁移信息更加丰富。同时，DFA将状态区分为接受状态和拒绝状态（表示某个string是否被正则语言L接受），而Mealy Machine中的状态全部为接受状态，仅依据状态迁移过程中的输入输出序列区分状态。

可以看出，相比于DFA，Mealy Machine更适合表示协议状态机，因为协议是根据输入而响应，并且转移到下一个状态的模型。Mealy Machine应用于协议状态机的形式化描述时，I和O分别对应于抽象出来的输入和输出报文类型集，一个会话对应于一个I/O序列。

L*算法

L*算法于1987年由耶鲁大学教授Dana Angluin提出，详见Learning Regular Sets from Queries and Counterexamples*。该算法的目标是通过不断请求和猜想，推断出目标黑盒系统的最小化DFA。

成员查询和等价查询

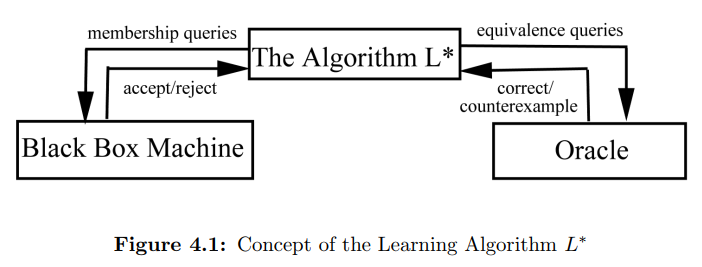
• membership query：一个来自Σ*中的string是否存在于目标正则语言中。每次查询返回的结果是1（accepted）或者0（rejected）。当通过成员查询完成了一个符合规范的观察表OT时，算法猜想出一个可能的状态机模型M。
• equivalence query：通过向teacher（也有称作oracle）发起等价查询来验证上述猜测的模型M是否与黑盒系统一样。若teacher发现了一个反例（counterexample），则将反例返回给Learner，扩展OT表，并开启新一轮学习，直到teacher找不到反例为止。反例是一个被M接受但是被目标黑盒系统（SUT）拒绝的string，或者相反。被目标系统接受，说明string的字符序列使状态机达到了最终接受状态F；被目标系统拒绝，说明string的字符序列使状态机达到中间某状态，但并非最终接受状态。

关于该算法Learner的行为描述（摘自参考文献5）：

The typical behavior of a Learner is to start by asking a sequence of membership queries, and gradually build a hypothesized DFA M using the obtained answers. When the Learner feels that she has built a “stable” hypothesis M, she makes an equivalence query to find out whether M is correct. If the result is successful, the Learner has succeeded, otherwise she uses the returned counterexample to revise M and perform subsequent membership queries until arriving at a new hypothesized DFA, etc.

Observation Table（OT表）

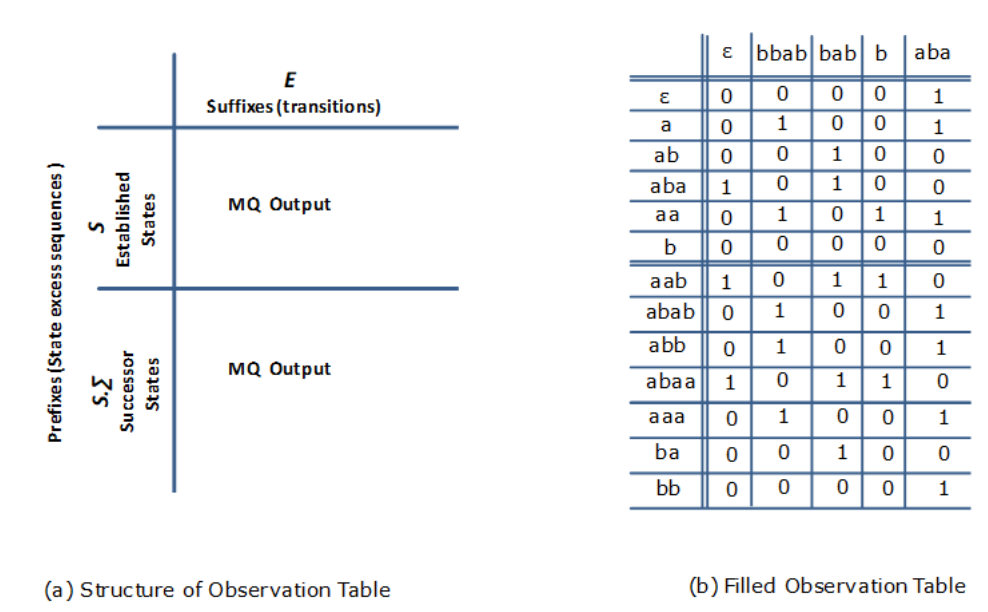
L*算法根据输出填充OT表。OT表中的概念：

• S：字母表Σ表示下的前缀闭合的字符串集合。预示当前学习程度中可能的状态。个人认为，保证S前缀闭合是为了避免跳过一些可能的状态，保持状态的连续性。
• E：字母表Σ表示下的后缀闭合的字符串集合。E可以用来区分S状态。
• S中元素s和E中元素e组成的字符串t = s·e，表示要向SUT查询的一个字符串。
• OT表的行标签分为两部分，一部分为S，表示当前学习到的Model的状态，另一部分为S·Σ，用来表示状态的转移。行标签合并表示为S∪S·Σ。
• OT表的列标签为E，用来区分不同的状态。
• T为映射函数，T = (S∪S·Σ)×E -> {0,1}，表示某个字符串t=s·e是否在SUT中存在（T(s,e)），通过membership query实现。如果字符串s·e被自动机D接受，则T(s,e)=1，否则=0。T函数的值就是OT表中需通过membership query查询的每个entry，每个entry就代表着learner向SUT查询过该对应string是否存在于正则语言L中。
• 等价的定义：对于正则语言L，x和y是L中字符串（x,y∈Σ*），如果x，y等价，则对于Σ*中的任何串z，xz和yz要么都是L的句子，要么都不是L的句子。但是，在OT表的构建过程中，不可能总是遍历Σ*中的所有字串来判断等价关系。因此，需要在OT表的范围内约定一个等价的定义，即：假定s,t∈S∪S·Σ为OT表的两个行标签，s和t等价（s≌t）当且仅当对于所有的e∈E，T(s,e) = T(t,e)。相当于把Σ*中的任意串作为后缀改为了OT表列标签E中的任意项作为后缀，缩小了范围。因此，无法完全判断s和t究竟是否真的等价，但是可以通过一致性检查确定它们一定不等价。
• 需注意，在构建OT表的过程中，row(a)=row(b)表示a，b等价，它们属于同一个等价类（equivalence class），但是也只是临时的等价，如果经过一致性检查发现它们不等价，那么需要将它们变成两个新的class。

OT表的闭合性和一致性

• 闭合性（closed）：对于每一个t∈S⋅Σ，在S中都有一个对应的s使得row(s) = row(t)，我们称观察表（S,E,row）闭合。即rows(S·Σ)⊆rows(S)。意思是S·Σ域中每一行，在S域中都能找到对应的等价项。个人理解：闭合性含义是当前没有新的状态出现。
• 一致性（consistent）：如果每当有 w1,w2 ∈ S，有row(w1) = row(w2)，然后对于所有的 a∈Σ，有row(w1·a) = row(w2·a)，我们就称观察表是一致的。即row(s)=row(s’) => row(s·a)=row(s’·a)。意思是对于两个状态，如果它们等价，那么添加相同的后缀所组成的状态也一定等价。个人理解：这两个状态是等价的两个状态，可以合并。

个人理解：当L*算法认为推断出来的模型没有新状态产生，并且对于看上去相同的状态也可以确定它们是完全一致的（同一个等价类），就会认为猜测出了一个可能的Model。

• 对于闭合性的检查，其目的是为了保证S·Σ中每一项都在S中有属于同一个等价类的项，并保证当前没有新的等价类出现，这样一来，在最后构建状态机时，就可以知道不同的状态转移（S·Σ中的行）会转移到具体哪个状态（S中对应的等价类状态）。
• 对于一致性的检查，其目的是为了保证S中每个等价类中的各项（状态）是真实等价的（个人认为，不能完全保证），即它们属于唯一的等价类，这样S·Σ中的状态转移才能对应到具体的某个确定的状态。

学习过程

• 当L*发现S中的s1和s2、E中的e以及Σ中的a，满足row(s1)=row(s2)但是T(s1·a·e)≠T(s2·a·e)，那么当前OT不是一致的，即两个所谓的等价类其实不是等价的。L*将a·e添加到E中，扩展并填充OT，用a·e来将两个等价类区分（distinguish）为两个新类。
• 当L*发现对于S·Σ中的t，满足row(t)和S中所有s的row(s)都不同，那么当前OT不是闭合的，表示存在新的状态。L*将t添加进S中，扩展并填充OT。扩展时将OT扩展至(S∪S·Σ)，也就是说，把t放入S之后，把t·a放入S∪Σ，其中a为Σ中所有项。因为如果row(t)和所有row(s)都不同，那么t可能是一个新的状态。
• 当L*认为OT已经满足一致性和闭合性，则认为猜想出一个Model M=(S,E,T)。
• 向teacher发起equivalence query，teacher检查M，如果发现并返回反例t，那么将t以及其前缀添加到S，并扩展S∪S·Σ，用成员查询扩展OT。重复上面步骤。
• 当teacher回复yes，则结束。

例子

来自参考文献3。DFA D如下图所示：

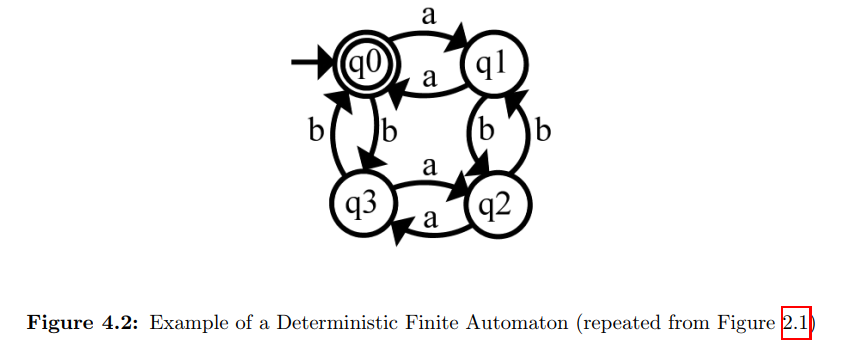
该DFA接受的正则语言L：所有包含偶数个（包括0）a以及偶数个（包括0）个b的字符串，其中q0为初始状态，也为结束状态，Σ = {a,b}。现在利用L*算法推测该DFA。首先构造初始OT表，如下图：

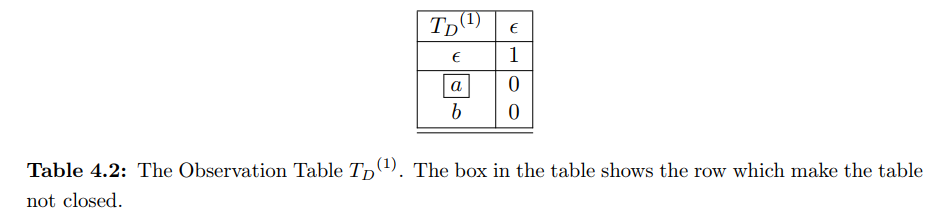
当前OT表是一致的（S中只有一项，不涉及等价的两项），但是并不闭合（row(a)≠row(ε)）。此时需要将S·Σ中的a添加到S当中，作为一个新的潜在状态。添加之后，S扩充为{ε,a}，接下来还要扩充S·Σ，将a·a和a·b添加到S·Σ当中。然后向SUT发起membership query，填充OT。填充后的OT如下图（左）所示：

当前OT是闭合（row(b)=row(a·b)=row(a)，row(a·a)=row(ε)）且一致（S中没有完全等价的两个row）的。因此算法认为猜测出来一个Model M1，如上图右所示。该M1包括两个状态。这里可以看到，b·b的结果其实是未知的。

接下来，Learner向teacher发起equivalence query。发现存在反例b·b，δ(q0,b·b)在teacher中返回q0（即[ε]），而在M1中返回到[a]。因此，L*将做以下三件事：

• 将反例b·b添加到S中
• 同时还要将其前缀（b）也一并添加到S中，保持S的前缀闭合
• 扩展S·Σ，添加b·a、b·b·a以及b·b·b到S·Σ
• 向SUT发起membership query，填充OT

经过上述步骤后，OT表被更新为如下所示：

可以看出，当前OT表为闭合的（S·Σ中所有row都能在S中找到对应等价项），但是不一致（row(a)和row(b)相同，但是T(a·a,ε)≠T(b·a,ε)）。算法将区分row a和row b的后缀a·ε=a添加仅E当中，并通过membership query填充OT。填充后的OT如下图所示：

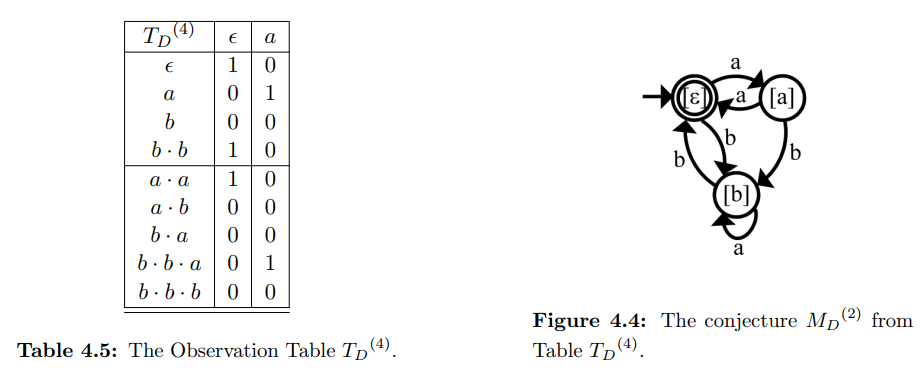
可以看出来，此时OT是闭合且一致的。算法推测出右图的状态机M2。这里状态机的构建可遵循以下几点考虑：

• 这里由于row(ε)和row(b·b)等价，它们在闭合且一致的条件下可以看做同一个状态，因此合并
• E用来区分不同的状态，row(ε)={1,0}，row(a)={0,1}，row(b)={0,0}为三个不同的状态，其中row(ε)为起始状态，图中标记为[ε]。
• S∪S·Σ中与上述三个状态等价的项，可以看做通过S∪S·Σ中的前缀转移到的同一个状态，如row(a·b)=row(b)，表示从初始状态经过a和b的输入，转移到了状态[b]，而row(a·a)=row(ε)表示从初始状态经过两次输入a，重新回到了初始状态

接下来进行equivalence query，teacher返回了反例a·b·b。因为在M2下，δ(q0,a·b·b)=q0，但在原始DFA中，a·b·b并不会使状态机回到初始状态q0。将a·b·b及其所有前缀添加到S中，由于a已经在S中，因此将a·b和a·b·b添加到S中。之后扩展S·Σ，添加a·b·a，a·b·b·a，a·b·b·b。填充OT，结果如下表所示：

当前OT是闭合的，但是并不一致，因为b和a·b等价，但是T(b·b,ε)≠T(a·b·b,ε)。因此，将后缀b·ε=b添加到E中，并填充OT，结果如下图左所示：

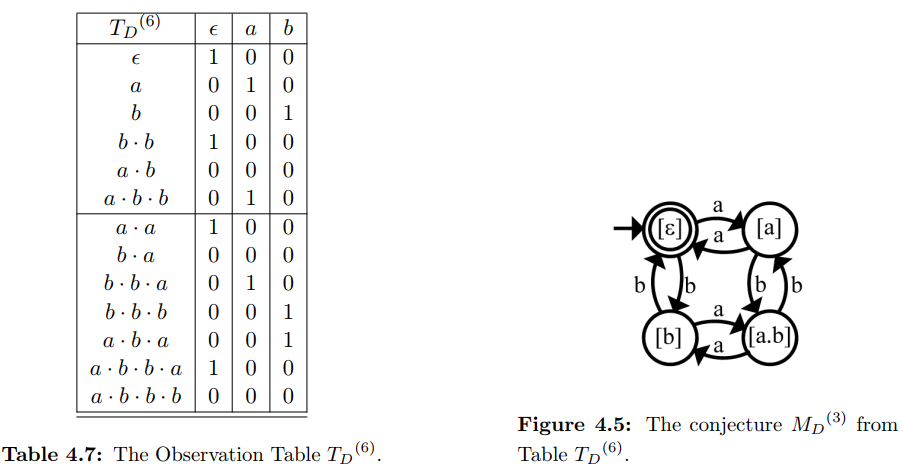
经过验证，该OT是一致且闭合的，于是算法推测出新的模型M3，如上图右所示。模型构建时，根据等价类进行，S中等价的两行可以合并为同一个状态，而S·Σ中某项t与S某项s相同，表示经过t转换后，达到了s对应的状态。

再次向teacher发起equivalence query，teacher返回yes，表示认可当前模型。L*算法将该DFA状态机模型返回给用户，完成DFA的构建。

总结

L*算法，其实就是一个用反例来引导，不断发现新的状态，并不断合并等价状态的过程。 L*算法只适合推断DFA，但是并不适合推断Mealy Machine。一些其他的算法如LM*算法、TTT算法支持推断Mealy Machine，之后继续学习。